분할 정복 (Divide & Conquer)

분할정복(Divide and Conquer)은 말 그대로 문제를 분할한 다음, 분할한 문제들 (sub-problems)을 해결하고, 그 결과를 합쳐서 원래의 문제를 해결하는 것입니다.
분할정복의 대표적인 예로는 합병 정렬, 고속 푸리에 변환 등이 있습니다.

합병정렬을 예로 설명해보겠습니다.
영역을 나눈 후, 나누어진 영역을 투 포인터(Two Pointer) 알고리즘으로 합병하는 방식으로 동작합니다.
투 포인터 알고리즘을 사용하려면 나눠진 영역이 정렬이 되어있어야 하기 때문에 먼저 영역을 작게 나눈 후 합치는 재귀적인 방법이 사용됩니다.

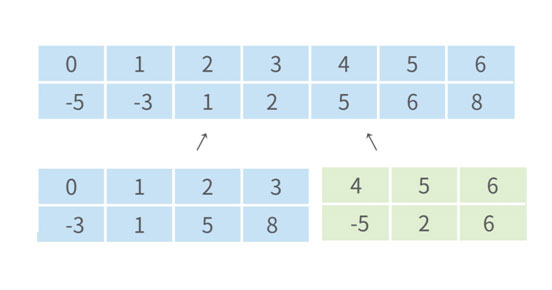
이진탐색과 유사하게 전체 영역을 [L, R], M = (L + R) / 2이라고 할 때 [L, M], [M+1, R] 두 개의 영역으로 분할하겠습니다.

[0, 3] [4, 6] 으로 분할

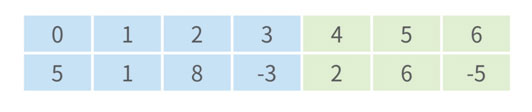
왼쪽 부분을 다시 분할해 보겠습니다.

[0, 1] [2, 3] 으로 분할

분할한 문제가 해결이 쉽게 가능할 때까지 분할합니다.

[0, 0] [1, 1] 로 분할

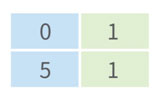
위와 같이 [0,0] , [1,1]로 분할된 영역을 투 포인터 알고리즘으로 합병합니다.

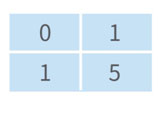
위와 마찬가지로 [2,3]도 합병한 후, 투 포인터 알고리즘으로 상위 [0,3]을 합병합니다.

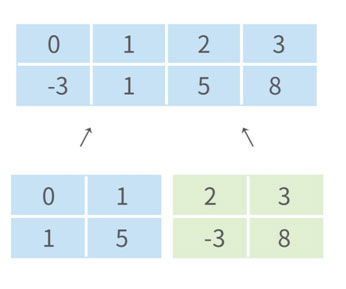
마지막으로 전체 영역을 합병합니다.

위의 분할 정복의 시간 복잡도는 최대 분할 * 합병 = O(log N) * O(N) = O(N log N)으로 상당히 빠르므로 효율적인 알고리즘으로 볼 수 있습니다.

위의 문제처럼 문제를 쉽게 해결 가능한 문제가 될 때까지 나눈 후 해결하고 합치는 과정을 반복하는 해법을 분할정복이라고 합니다.
위의 경우에는 분할된 문제(sub-problem)이 중복이 되지 않지만 피보나치를 구하는 문제는 분할된 문제가 중복이 되는 경우가 있습니다.

위의 음영 처리된 부분은 중복된 sub-problem으로 이를 분할할 때마다 처리한다면 매우 비효율적일 것입니다.
이와 같은 문제는 분할정복보다는 동적계획법의 Top-Down 접근법(Memoization)으로 접근하는 것이 효율적일 것입니다.

다음은 C++로 나타낸 합병정렬의 코드입니다.

#include <iostream>

#define MAX 5005

using namespace std;

int d[MAX];
int temp[MAX];

void MergeSort(int L, int R) {
	if (L >= R) return;

	int M = (L + R) / 2;

	// Divide

	MergeSort(L, M);
	MergeSort(M + 1, R);

	// Conquer

	for (int i = L, l = L, r = M + 1;
		l != M + 1 || r != R + 1;
		i++) {

		if ((r != R + 1 && l <= M && d[l] < d[r]) || r == R + 1)
			temp[i] = d[l++];
		else
			temp[i] = d[r++];
	}

	for (int i = L; i <= R; i++)
		d[i] = temp[i];
}

int main() {
	int n;

	cin >> n;

	for (int i = 0; i < n; i++)
		cin >> d[i];

	MergeSort(0, n - 1);

	for (int i = 0; i < n; i++)
		cout << d[i] << " ";
}

다음은 Java로 나타낸 합병정렬 코드입니다.

import java.util.*;

public class Main {
	public static void main(String args[]){
		Scanner scanner = new Scanner(System.in);
		int n = scanner.nextInt();

		int [] d = new int[5005];
    
		for (int i = 0; i < n; i++)
			d[i] = scanner.nextInt();

		mergesort(d, 0, n - 1);
		
		for(int i = 0 ; i < n ; i++)
			System.out.print(d[i] + " ");
	}
	
	static void mergesort(int[]d, int L, int R){
		if(L >= R) return;
		int M = (L + R) / 2;

		mergesort(d, L, M);
		mergesort(d, M + 1, R);
		
	    ArrayList <Integer> temp = new ArrayList<>();

		for (int i = L, l = L, r = M + 1;
			l != M + 1 || r != R + 1;
			i++) {

			if ((r != R + 1 && l <= M && d[l] < d[r]) || r == R + 1) 
				temp.add(d[l++]);
			else
				temp.add(d[r++]);
		}

		for (int i = L; i <= R; i++)
			d[i] = temp.get(i - L);	
	}
}