슬라이딩 윈도우(Sliding Window)
슬라이딩 윈도우(Sliding Window) 알고리즘은 투 포인터(Two Pointers) 알고리즘과 유사하게 동작하지만, 두 개의 포인터 사이의 길이가 고정되어 있다는 차이점이 존재합니다.
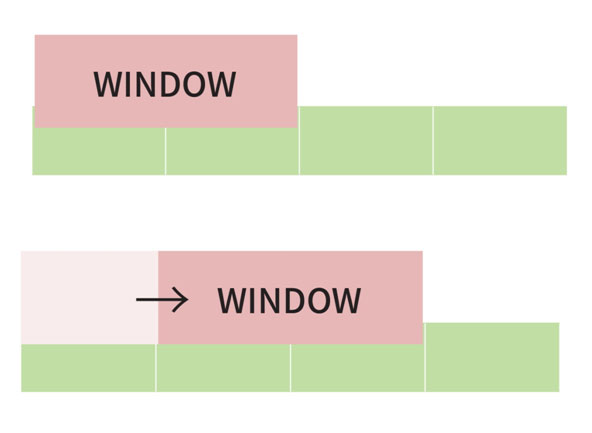
위의 그림과 같이 모든 영역을 고정된 영역을 만든 후, 한 칸씩 밀면서 테스팅 해보는 방법입니다.
이를 통해 길이가 고정된 모든 연속 부분집합들의 누적합, 최댓값, 최솟값을 구할 수 있습니다.
간단히 누적합을 생각해보면, 윈도우를 한 칸 밀 때마다 기존 윈도우의 합에서 윈도우의 오른쪽 방향의 값을 더하고 윈도우에서 빠진 한 칸을 빼주면 각 창마다의 누적합을 구할 수 있습니다.
이 경우의 시간 복잡도는 O(N)이 됩니다.
길이가 고정된 모든 연속 부분집합들의 최댓값을 구하는 방법은 우선순위큐(Priority Queue, 또는 힙)를 추가하면 슬라이딩 윈도우 알고리즘으로 해결할 수 있습니다.
먼저 윈도우에 포함된 원소를 우선순위큐에 추가합니다.
여기서 값과 함께 해당 데이터의 인덱스도 함께 추가합니다.
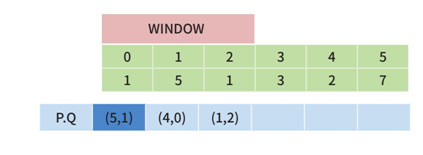
이 윈도우에 해당되는 구간인 [0,2]의 최댓값은 우선순위큐의 Top인 5이며 이 5의 인덱스는 1입니다. 윈도우를 한 칸 옮겨보도록 하겠습니다.
먼저 예상을 해보자면, 우선순위큐에는 3번지에 있는 3이 추가가 될 것입니다.
하지만, 윈도우의 처음 부분인 4가 삭제가 되어야 할 것입니다. 그래야 윈도우를 제대로 옮기는 것이기 때문입니다.
하지만, 우선순위큐는 Top 이외의 원소를 탐색하는 시간 복잡도는 O(N)으로 매우 느리기 때문에 다른 방식을 생각해보아야 합니다.
잘 생각해보면, 문제 해결에 필요한 데이터는 최댓값뿐입니다.
삭제되어야 할 원소가 최댓값이 아니라면, 삭제를 하지 않아도 됩니다.
만약 우선순위큐의 Top의 원소와 함께 넣어둔 인덱스가 현재 윈도우 인덱스에 포함되지 않는다면 Pop을 하여 윈도우 내의 범위 원소가 나올 때까지 반복하면 됩니다.
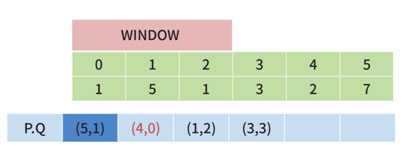
윈도우를 한 칸 민 후의 상태입니다.
(5,1)은 윈도우의 범위에 포함되기에 문제가 발생하지 않습니다.
윈도우를 한 칸 더 밀어 다음 원소를 우선순위 큐에 넣어보겠습니다.
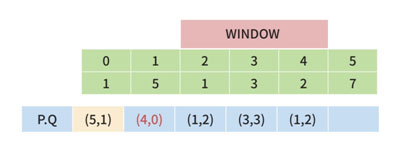
여기서 우선순위큐의 Top은 윈도우의 범위를 벗어납니다. 그렇기 때문에 Pop을 합니다.
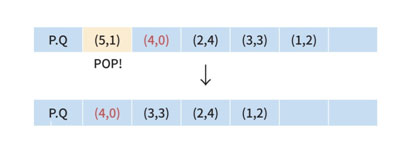
또 다시 범위를 벗어나기 때문에 다시 Pop을 합니다.
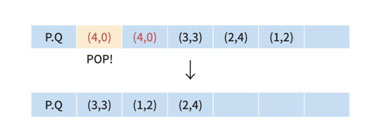
이제는 우선순위큐에 해당 윈도우의 값만 존재합니다.
물론 우선순위 큐 내에 해당 윈도우 이외의 값이 존재할 수는 있지만, 우리가 구하려는 값과는 관계가 없습니다.
앞으로 이 과정을 반복하면 길이가 고정된 모든 구간에 대한 최대값을 구할 수 있습니다.
위와 같이 슬라이딩 윈도우는 순차적인 접근을 가지는 특징을 가진 문제에서 부분적으로 사용됩니다.
구현이 쉽고 시간 복잡도를 줄일 수 있기 때문에 유용한 알고리즘 중 하나입니다.
아래 코드는 처음 언급한 누적합 문제에 대한 코드입니다.
import java.util.*;
public class Main {
public static void main(String args[]) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int k = scanner.nextInt();
ArrayList<Integer> d = new ArrayList<>();
for (int i = 0; i < n; i++)
d.add(scanner.nextInt());
int sum = 0, max = 0;
for (int i = 0; i < n; i++) {
if (i < k) sum += d.get(i);
else sum = sum - d.get(i - k) + d.get(i);
max = (max < sum) ? sum : max;
}
System.out.println(max);
}
}