플레인 스위핑(Plane sweeping)
플레인 스위핑(Plane sweeping)은 직각 도형의 넓이를 구할 때 주로 쓰이는 알고리즘입니다.
작은 범위는 flood-fill 을 사용하여 배열을 원하는 격자만큼 그린 후, 도형의 넓이를 직접 배열에 칠해가며 해결할 수 있지만, 범위가 커진다면 메모리와 시간 모두 문제가 생기기 때문에 다른 방법을 찾아야만 합니다. 플레인 스위핑은 이를 해결할 수 있는 방법 중 하나입니다.
먼저 2개의 직사각형의 그림자의 넓이를 구해보겠습니다. 먼저 직사각형은 왼쪽 아래와 오른쪽 위 두 점으로 주어집니다. 두 개의 직사각형은 겹친 부분이 있기 때문에, 단순 공식에 의한 직사각형 넓이의 합으로 구하기 어렵습니다.
플레인 스위핑은 위 문제에서 사용되는 좌표들은 한정됨을 이용합니다.
각 직사각형들은 4개의 꼭짓점을 가지고, 이 꼭짓점들의 좌표는 x, y축 각각 2개씩으로 조합이 됩니다. N개의 직사각형이라면 좌표의 범위와 상관없이 최대 N * 2개의 x좌표와 N*2개의 y좌표가 사용됨 을 알 수 있습니다.
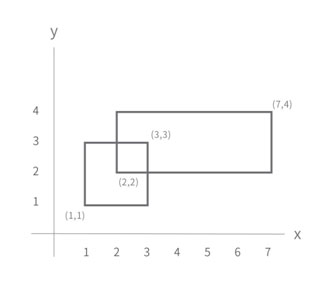
우리는 사용되는 좌표 이외의 좌표를 몰라도 위의 넓이를 계산할 수 있습니다.
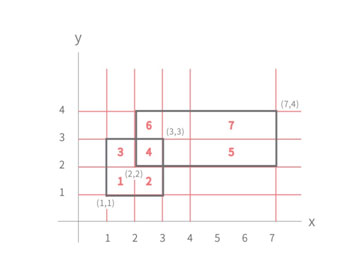
위와 같이 우리가 사용하는 좌표만으로 격자를 쪼갠 후, 직사각형 부분을 계산해 나갑니다.
1번의 직사각형의 넓이는 가로 * 세로 = (2-1)*(2-1) 로 구할 수 있습니다.
마찬가지로 2 ~ 7번까지 모든 영역을 구할 수 있습니다. 이 모든 구역의 합이 정답이 될 것입니다.
이를 구현하는 과정은 다음과 같습니다.
먼저 사용되는 X, Y좌표를 모두 구한 후 정렬합니다. (원소들이 꼭 유니크할 필요는 없습니다)
그 후 X, Y좌표로 잘려진 영역을 차례로 순회하면서 주어진 사각형 중 하나라도 영역이 포함되면 더해줍니다. (이때 원소들이 유니크하지 않다면, 정렬이 되었기 때문에 같은 값이 붙어 있을 것이고, 그 영역의 넓이는 당연히 0이 되므로 생각하지 않으셔도 좋습니다.)
이 과정에 세그먼트 트리를 사용해서 구간 갱신 속도 등을 줄여 시간 복잡도를 대폭 단축시킬 수 있기 때문에 함께 쓰는 연습도 하는 것이 좋습니다.
다음은 위와 유사한 문제를 작성한 코드입니다. 왼쪽 아래점을 기준으로 너비와 폭이 주어지고, 그 넓이를 구하는 코드입니다.
| 입력 | 출력 |
| 첫 번째 줄에 사각형의 수 N이 입력된다. 2 ~ N + 1번째 줄에 차례대로 사각형의 왼쪽 아래점 X좌표, Y좌표, 높이, 너비가 주어진다 |
주어진 직사각형들의 그림자의 넓이를 구한다. |
| Sample Input | Sample output |
| 2 1 1 2 2 2 2 3 3 |
12 |
import java.util.*;
public class Main {
public static void main(String args[]) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int ans = 0;
ArrayList<rect> d = new ArrayList<>();
ArrayList<Integer> x = new ArrayList<>();
ArrayList<Integer> y = new ArrayList<>();
for (int i = 0; i < n; i++) {
rect t = new rect();
t.x = scanner.nextInt();
t.y = scanner.nextInt();
t.width = scanner.nextInt();
t.height = scanner.nextInt();
d.add(t);
x.add(d.get(i).x);
x.add(d.get(i).x + d.get(i).width);
y.add(d.get(i).y);
y.add(d.get(i).y + d.get(i).height);
}
Collections.sort(x);
Collections.sort(y);
for (int i = 0; i < x.size() - 1; i++)
for (int j = 0; j < y.size() - 1; j++)
for (int k = 0; k < n; k++)
if (x.get(i) >= d.get(k).x && x.get(i + 1) <= d.get(k).x + d.get(k).width &&
y.get(j) >= d.get(k).y && y.get(j + 1) <= d.get(k).y + d.get(k).height) {
ans += (x.get(i + 1) - x.get(i)) * (y.get(j + 1) - y.get(j));
break;
}
System.out.println(ans);
}
static class rect {
int x, y, width, height;
rect(){}
}
}