BFS (Breadth-First Search, 너비 우선 탐색)
너비 우선 탐색은 그래프의 모든 정점들을 특정한 순서에 따라 방문하는 알고리즘 중 하나입니다. 현재 정점과 인접한 간선들을 검사하다가 방문하지 않은 정점들을 발견하면 그 간선을 통해 방문하지 않은 정점들을 자료구조 큐에 넣습니다. 그리고 큐의 front 정점을 방문하고 pop합니다.
또 해당 정점에서 인접한 간선을 검사해 방문하지 않은 정점들을 큐에 넣고 방문하기는 과정을 반복하다가 더 이상 방문할 수 있는 정점이 없으면 종료합니다. 이러한 과정을 반복하여 큐에 더 이상 정점이 존재하지 않을 때까지 실행하여 그래프의 모든 정점을 방문하는 알고리즘이 BFS 알고리즘입니다
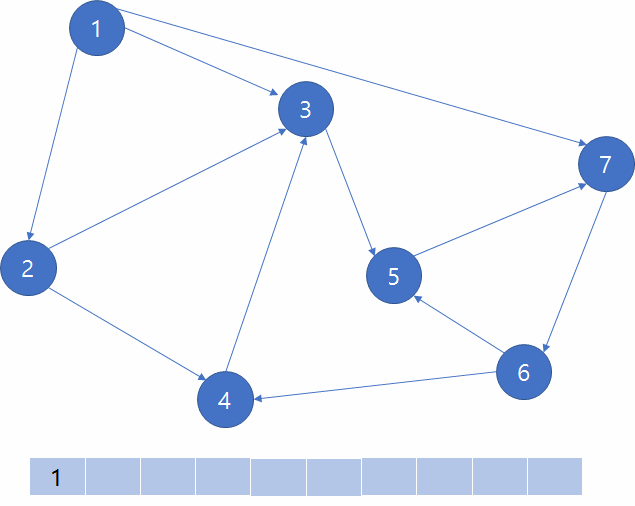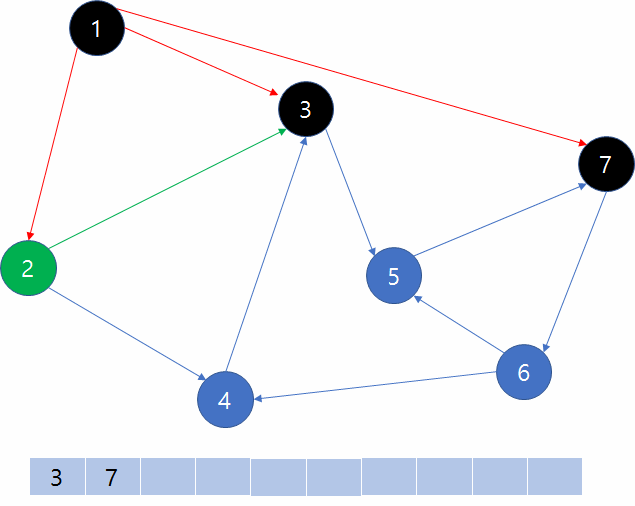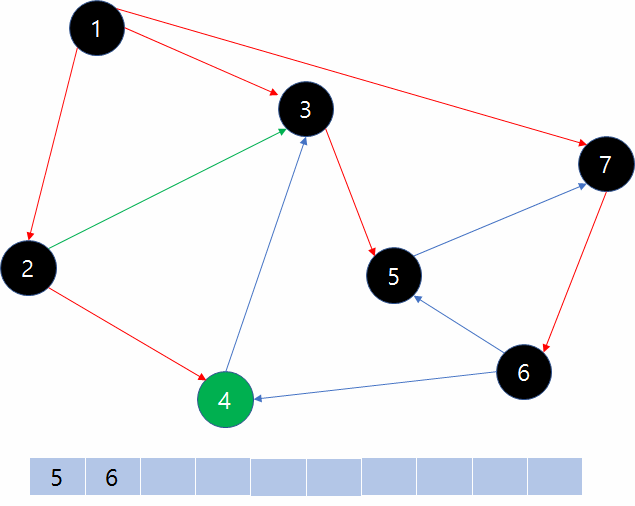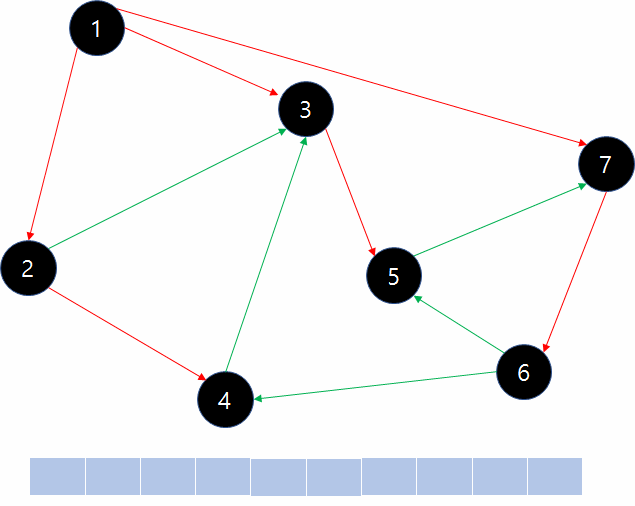

위의 그림과 같은 유향 그래프가 존재하고 한 정점에서 여러 개의 정점으로 이동이 가능할 때 정점의 번호가 더 작은 쪽을 먼저 방문한다고 가정을 하겠습니다. 이 때, 정점 1에서 너비 우선 탐색을 하게 된다고 합시다. 큐에 정점 1을 넣습니다.
그리고 큐의 front인 정점 1을 현재 정점으로 놓고 큐를 pop합니다. 정점1과 연결된 간선들을 통해 연결된 정점을 확인하면 2,3,7이 연결되어 있습니다. 이 때, 정점의 번호가 작은 쪽을 방문한다는 규칙에 의해 2를 먼저 큐에 넣어줍니다. 그리고 마찬가지로 3번 7번 정점도 큐에 넣어줍니다. 3개의 정점 모두 방문했다고 처리해줍니다. 그러면 다음으로 큐의 front인 2번 정점이 현재 정점이 됩니다. 마찬가지로 큐를 pop합니다. 3,4로 이동할 수 있지만 3번은 이미 방문처리가 된 정점이며 큐에 이미 들어있기 때문에 4번 정점을 큐에 넣어줍니다.
이와 같은 식으로 규칙대로 이동하다보면 1-2-3-7-4-5-6와 같이 방문을 하게됩니다. 6번 정점은 4번 정점과 5번 정점과 연결되어 있으나 이미 방문된 정점들이므로 이동할 수 없습니다. 따라서 큐에는 더 이상 정점들이 존재하지 않게 되고 BFS는 끝나게 됩니다. 이 순서는 결과적으로 시작점과 가까운(이동에 필요한 간선의 수가 적은) 정점 순서로 방문하는 것이 됩니다.
해당 알고리즘을 구현하기 위해서는 해당 정점이 방문되었는지 확인하는 boolean타입의 1차원 배열과 정점들의 집합 그리고 정점과 정점 사이의 연결을 확인할 수 있는 간선 집합들이 필요합니다.
그리고 해당 알고리즘의 시간복잡도는 모든 정점을 방문하며 모든 간선을 검사하기 때문에 시간복잡도는 O(V+E)입니다. ( V: 정점의 개수, E: 간선의 개수)
다음은 C++로 나타낸 코드입니다.
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
vector<vector<int> > edge;
vector<bool> visited;
int N, M;
int u, v;
void bfs(int cur) {
queue<int> q;
visited[cur] = true;
q.push(cur);
while (!q.empty()) {
int here = q.front();
q.pop();
cout << here << ' ';
for (int i = 0; i < edge[here].size(); i++) {
int there = edge[here][i];
if (visited[there]) continue;
visited[there] = true;
q.push(there);
}
}
}
int main() {
cin >> N >> M;
edge.resize(N + 1);
visited.resize(N + 1);
for (int i = 0; i < M; i++) {
cin >> u >> v;
edge[u].push_back(v);
}
bfs(1);
}다음은 Java로 나타낸 코드입니다.
import java.util.*;
public class Main {
static boolean edge[][];
static boolean visited[];
static int n;
static int m;
public static void main(String args[]) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
m = scanner.nextInt();
edge = new boolean[n + 1][n + 1];
visited = new boolean[n + 1];
for (int i = 0; i < m; i++) {
int u = scanner.nextInt();
int v = scanner.nextInt();
edge[u][v] = true;
}
bfs(1);
}
public static void bfs(int cur) {
Queue<Integer> q = new LinkedList<>();
visited[cur] = true;
q.add(cur);
while (!q.isEmpty()) {
int here = q.remove();
System.out.print(String.valueOf(here) + ' ');
for (int there = 1; there <= n; there++) {
if (visited[there] || (!edge[here][there])) continue;
visited[there] = true;
q.add(there);
}
}
}
}